In mathematics and statistics, the line that demarcates sequence and series are thin and blurred, due to which many think that these terms are one and the same thing. Nevertheless, the notion of sequence differs from series in the sense that sequence refers to an arrangement in the particular order in which related terms follow each other, i.e. it has an identified first unit, second unit, third unit and so forth.
When a sequence follows a particular rule, it is called as progression. It is not exactly same as series which is defined as the summation of the elements of a sequence. Take a read of the article to know the significant difference between sequence and series.
Content: Sequence Vs Series
Comparison Chart
| Basis for Comparison | Sequence | Series |
|---|---|---|
| Meaning | Sequence is described as the set of numbers or objects that follows a certain pattern. | Series refers to the sum of the elements of the sequence. |
| Order | Important | Sometimes important |
| Example | 1, 3, 5, 7, 9, 11....n.. | 1 + 3 + 5 + 9 + 11...n.. |
Definition of Sequence
In mathematics, an ordered set of objects or numbers, like a1, a2, a3, a4, a5, a6……an…. are said to be in a sequence, if, as per certain rule, has a definite value. The members of the sequence are called term or element which is equal to any value of the natural number. Every term in a sequence is related to the preceding and succeeding term. In general, sequences have a hidden rules or pattern, which helps you find out the value of the next term.
The nth term is the function of integer n (positive), regarded as the general term of the sequence. A sequence can be finite or infinite.
- Finite Sequence: A finite sequence is one that stops at the end of the list of numbers a1, a2, a3, a4, a5, a6……an, is represented by:
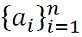
- Infinite Sequence: An infinite sequence refers to a sequence which is unending, a1, a2, a3, a4, a5, a6……an….., is represented by:
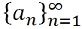
Definition of Series
The addition of the terms of a sequence (an), is known as series. Like sequence, series can also be finite or infinite, where a finite series is one that has a finite number of terms written as a1 + a2 + a3 + a4 + a5 + a6 + ……an. Unlike infinite series, where the number of elements are not finite or which are unending, written as a1 + a2 + a3 + a4 + a5 + a6 + ……an +….
If a1 + a2 + a3 + a4 + a5 + a6 + …… an = Sn, then Sn is considered as the sum to n elements of the series. The sum of terms is often represented by Greek letter sigma (Ʃ). Hence,
Key Differences Between Sequence and Series
The difference between sequence and series can be drawn clearly on the following grounds:
- The sequence is defined as the collection of numbers or objects that follow a definite pattern. When the elements of the sequence are added together, they are known as series.
- Order matters in a sequence, as there is a certain rule that prescribes the pattern of the sequence. Hence, 1, 2, 3three is different from 3, 1, 2. On the other hand, in a series order of appearance may or may not matter, like in the case of absolutely convergent series the order doesn’t matter. So, 1 + 2 + 3 is same as 3 + 1 + 2, only their sequence is different.
Conclusion
Arithmetic Progression (A.P.) and Geometric Progression (G.P.) are also sequences, not series. Arithmetic Progression is a sequence in which there is a common difference between the consecutive terms such as 2, 4, 6, 8 and so on. On the contrary, in a geometric progression, each element of the sequence is the common multiple of the preceding term such as 3, 9, 27, 81and so on. Similarly, Fibonacci Sequence is also one of the popular infinite sequence, in which each term is obtained by adding up the two preceding terms 1, 1, 3, 5, 8, 13, 21 and so on.
sarath chandran says
I found the page to be informative, thank you.