Difference Between Binomial and Poisson Distribution

The binomial distribution is one, whose possible number of outcomes are two, i.e. success or failure. On the other hand, there is no limit of possible outcomes in Poisson distribution

The theoretical probability distribution is defined as a function which assigns a probability to each possible outcomes of the statistical experiment. The probability distribution can be discrete or continuous, where, in the discrete random variable, the total probability is allocated to different mass points while in the continuous random variable the probability is distributed at various class intervals.

Binomial distribution and Poisson distribution are two discrete probability distribution. Normal distribution, student-distribution, chi-square distribution, and F-distribution are the types of continuous random variable. So, here we go to discuss the difference between Binomial and Poisson distribution. Have a look.

Content: Binomial Distribution Vs Poisson Distribution

1. Comparison Chart
2. Definition
3. Key Differences
4. Conclusion

Comparison Chart

Basis for Comparison	Binomial Distribution	Poisson Distribution
Meaning	Binomial distribution is one in which the probability of repeated number of trials are studied.	Poisson Distribution gives the count of independent events occur randomly with a given period of time.
Nature	Biparametric	Uniparametric
Number of trials	Fixed	Infinite
Success	Constant probability	Infinitesimal chance of success
Outcomes	Only two possible outcomes, i.e. success or failure.	Unlimited number of possible outcomes.
Mean and Variance	Mean > Variance	Mean = Variance
Example	Coin tossing experiment.	Printing mistakes/page of a large book.

Definition of Binomial Distribution

Binomial Distribution is the widely used probability distribution, derived from Bernoulli Process, (a random experiment named after a renowned mathematician Bernoulli). It is also known as biparametric distribution, as it is featured by two parameters n and p. Here, n is the repeated trials and p is the success probability. If the value of these two parameters is known, then it means that the distribution is fully known. The mean and variance of the binomial distribution are denoted by µ = np and σ2 = npq.

P (X = x) = ⁿC_x p^x q^n-x, x = 0,1,2,3…n
= 0, otherwise

An attempt to produce a particular outcome, which is not at all certain and impossible, is called a trial. The trials are independent and a fixed positive integer. It is related to two mutually exclusive and exhaustive events; wherein the occurrence is called success and non-occurrence are called failure. p represents the probability of success while q = 1 – p represents the probability of failure, which does not change throughout the process.

Definition of Poisson Distribution

In the late 1830s, a famous French mathematician Simon Denis Poisson introduced this distribution. It describes the probability of the certain number of events happening in a fixed time interval. It is uniparametric distribution as it is featured by only one parameter λ or m. In Poisson distribution mean is denoted by m i.e. µ = m or λ and variance is labelled as σ² = m or λ. The probability mass function of x is represented by:

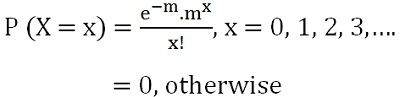where e = transcendental quantity, whose approximate value is 2.71828

When the number of the event is high but the probability of its occurrence is quite low, poisson distribution is applied. As for example, Number of insurance claims/day on an insurance company.

Conclusion

Apart from the above differences, there are a number of similar aspects between these two distributions i.e. both are the discrete theoretical probability distribution. Further, on the basis of the values of parameters, both can be unimodal or bimodal. Moreover, the binomial distribution can be approximated by the poisson distribution, if the number of attempts (n) tends to infinity and success probability (p) tends to 0 so that m = np.