 Central tendency implies the tendency of the data points to cluster around its central or middle-most value. The two most commonly used measures of central tendency are mean and median. Mean is defined as the ‘central’ value of the given set of data whereas median is the ‘middle-most’ value in the given set of data.
Central tendency implies the tendency of the data points to cluster around its central or middle-most value. The two most commonly used measures of central tendency are mean and median. Mean is defined as the ‘central’ value of the given set of data whereas median is the ‘middle-most’ value in the given set of data.
An ideal measure of central tendency is one which is clearly defined, easily understood, simply calculable. It should be based on all observations and least affected by extreme observations present in the set of data.
People often contrast these two measures, but the fact is that they are different. This article specifically highlights the basic differences between mean and median. Have a look.
Content: Mean Vs Median
Comparison Chart
| Basis for Comparison | Mean | Median |
|---|---|---|
| Meaning | Mean refers to the simple average of the given set of values or quantities. | Median is defined as the middle number in an ordered list of values. |
| What is it? | It is an arithmetic average. | It is positional average. |
| Represents | Center of gravity of data set | Center of gravity of data set Mid-point of data set |
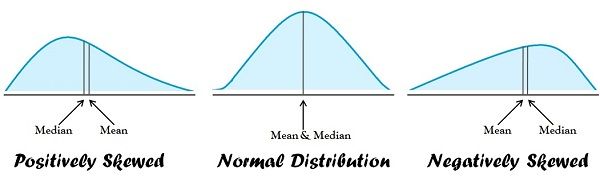
| Applicability | Normal distribution | Skewed distribution |
| Outliers | Mean is sensitive to outliers. | Median is not sensitive to outliers. |
| Calculation | Mean is calculated by adding up all the observations and then dividing the value obtained with the number of observations. | To calculate median, the data set is arranged in ascending or descending order, then the value that falls in the exact middle of the new data set, is median. |
Definition of Mean
The mean is the widely used measure of central tendency, which defined as the average of the set of values. It represents the model and the most common value of the given range of values. It can be calculated, both in discrete and continuous series.
The mean is equal to the sum of all observations divided by the number of observations in the dataset. If the value assumed by a variable is equal, its mean will also be same. Mean can be of two types, the sample mean (x̅) and population mean (µ). It can be calculated with given formula:
- Arithmetic mean:
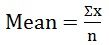 where Ʃ = Greek letter sigma, denotes ‘sum of..’
where Ʃ = Greek letter sigma, denotes ‘sum of..’
n = number of values - For Discrete Series:
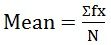 where, f = frequency
where, f = frequency - For Continuous Servies:
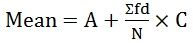 where d = (X-A)/C
where d = (X-A)/C
A = Assumed Mean
C = Common divisor
Definition of Median
The median is another important measure of central tendency, used to partition value into two equal parts, i.e. greater half of the sample, population or probability distribution from the lower half. It is the middle-most value, which is achieved when the observations are sorted in a specific order, either ascending or descending order.
For the calculation of median, first of all, arrange the observations in lowest to highest or highest to lowest, then apply the appropriate formula, as per the conditions are given below:
- If the number of observations is odd:
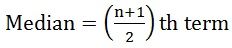 where n= number of observations
where n= number of observations - If the number of observations is even:
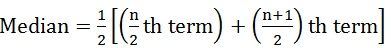
- For continuous series:
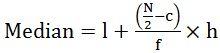 where, l = lower limit of the median class
where, l = lower limit of the median class
c = cumulative frequency of the preceding median class
f = frequency of the median class
h = class width
Key Differences Between Mean and Median
The significant differences between mean and median are provided in the article give below:
- In statistics, a mean is defined as the simple average of the given set of values or quantities. The median is said to be the middle number in an ordered list of values.
- While mean is the arithmetic average, the median is positional average, in essence, the position of the data set determines the value of median.
- Mean outlines the centre of gravity of data set whereas median highlights the middle-most value of the data set.
- The mean is appropriate for normally distributed data. On the other end, the median is best when the data distribution is skewed.
- The mean is highly affected by the extreme value which is not in the case with a median.
- The mean is calculated by adding up all the observations and then dividing the value obtained with the number of observations; the result is mean. As opposed to the median, the data set is arranged in ascending or descending order, then the value that falls in the exact middle of the new data set is median.
Example
Find the mean and median of the given set of data:
58, 26, 65, 34, 78, 44, 96
Solution: To compute mean, you need to divide the sum of observations with the number of observations,
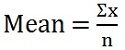
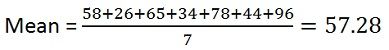 Mean = 57.28
Mean = 57.28
To calculate median, first of all, arrange the series in a sequence, i.e. lowest to highest,
26, 34, 44, 58, 65, 78, 96
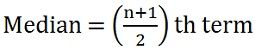 where n = number of observations
where n = number of observations
Conclusion
After reviewing the above points, we can say that these two mathematical concepts are different. Arithmetic mean or Mean is considered as the best measure of central tendency as it contains all the features of an ideal measure but it has one drawback that the sampling fluctuations influence the mean.
In the same way, the median is also unambiguously defined and easy to understand and calculate, and the best thing about this measure is that it is not affected by sampling fluctuations, but the only disadvantage of the median is that it is not based on all observations. For open end classification, the median is normally preferred over mean.
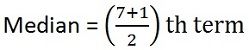





Sandeep says
Amazing and very cleared and helpful content 😊
Ana Carol says
Great article, Surbhi S! Thank you for explaining the Difference Between Mean and Median so clearly.