 Dispersion indicates the extent to which observations deviate from an appropriate measure of central tendency. Measures of dispersion fall into two categories i.e. an absolute measure of dispersion and relative measure of dispersion. Variance and standard deviation are two types of an absolute measure of variability; that describes how the observations are spread out around the mean. Variance is nothing but the average of the squares of the deviations,
Dispersion indicates the extent to which observations deviate from an appropriate measure of central tendency. Measures of dispersion fall into two categories i.e. an absolute measure of dispersion and relative measure of dispersion. Variance and standard deviation are two types of an absolute measure of variability; that describes how the observations are spread out around the mean. Variance is nothing but the average of the squares of the deviations,
Unlike, standard deviation is the square root of the numerical value obtained while calculating variance. Many people contrast these two mathematical concepts. So, this article makes an attempt to shed light on the important difference between variance and standard deviation.
Content: Variance Vs Standard Deviation
Comparison Chart
| Basis for Comparison | Variance | Standard Deviation |
|---|---|---|
| Meaning | Variance is a numerical value that describes the variability of observations from its arithmetic mean. | Standard deviation is a measure of dispersion of observations within a data set. |
| What is it? | It is the average of squared deviations. | It is the root mean square deviation. |
| Labelled as | Sigma-squared (σ^2) | Sigma (σ) |
| Expressed in | Squared units | Same units as the values in the set of data. |
| Indicates | How far individuals in a group are spread out. | How much observations of a data set differs from its mean. |
Definition of Variance
In statistics, variance is defined as the measure of variability that represents how far members of a group are spread out. It finds out the average degree to which each observation varies from the mean. When the variance of a data set is small, it shows the closeness of the data points to the mean whereas a greater value of variance represents that the observations are very dispersed around the arithmetic mean and from each other.
For unclassified data: 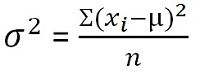
For grouped frequency distribution: 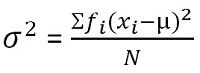
Definition of Standard Deviation
Standard deviation is a measure that quantifies the amount of dispersion of the observations in a dataset. The low standard deviation is an indicator of the closeness of the scores to the arithmetic mean and a high standard deviation represents; the scores are dispersed over a higher range of values.
For unclassified data: 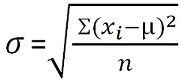 For grouped frequency distribution:
For grouped frequency distribution: 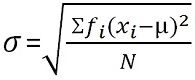
Key Differences Between Variance and Standard Deviation
The difference between standard deviation and variance can be drawn clearly on the following grounds:
- Variance is a numerical value that describes the variability of observations from its arithmetic mean. Standard deviation is a measure of the dispersion of observations within a data set relative to their mean.
- Variance is nothing but an average of squared deviations. On the other hand, the standard deviation is the root mean square deviation.
- Variance is denoted by sigma-squared (σ2) whereas standard deviation is labelled as sigma (σ).
- Variance is expressed in square units which are usually larger than the values in the given dataset. As opposed to standard deviation which is expressed in the same units as the values in the set of data.
- Variance measures how far individuals in a group are spread out in the set of data from the average. Conversely, Standard Deviation measures how much observations of a data set differs from its mean.
Illustration
Marks scored by a student in five subjects are 60, 75, 46, 58 and 80 respectively. You have to find out the standard deviation and variance.
First of all, you have to find out the mean,
So the average (mean) marks are 63.8
Now calculate the variance
| X | A | (x-A) | (X-A)^2 |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
Where, X = Observations
A = Arithmetic Mean
Similarities
- Both variance and standard deviation are always positive.
- If all the observations in a data set are identical, then the standard deviation and variance will be zero.
Conclusion
These two are basic statistical terms, which are playing a vital role in different sectors. Standard deviation is preferred over mean as it is expressed in the same units as those of the measurements while the variance is expressed in the units larger than the given data set.
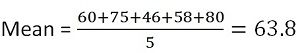





Ken says
Thank you for your effort
Anitha says
Well explained, thank you
komal says
thank you very much
NCW says
Can you explain variance and standard deviation by using values of above example?
Mohammed Hamid Azmi says
Very clear, good effort dear
RAJAN SEHGAL says
Explaining everything logical and simple way
clear all doubts and make concepts crystal clear