In statistic, the arithmetic mean is one of the ideal measures of central tendency. For a given set of observations, the arithmetic mean can be calculated by adding all the observations and dividing the value obtained by the number of observations. There are two types of mean, i.e. sample mean and population mean, which is often used in statistics and probability. The sample mean is mainly used to estimate the population mean when population mean is not known as they have the same expected value.
Sample Mean implies the mean of the sample derived from the whole population randomly. Population Mean is nothing but the average of the entire group. Take a glance at this article to know the differences between sample mean and population mean.
Content: Sample Mean Vs Population Mean
Comparison Chart
| Basis for Comparison | Sample Mean | Population Mean |
|---|---|---|
| Meaning | Sample mean is the arithmetic mean of random sample values drawn from the population. | Population mean represents the actual mean of the whole population. |
| Symbol | x̄ (pronounced as x bar) | μ (Greek term mu) |
| Calculation | Easy | Difficult |
| Accuracy | Low | High |
| Standard deviation | When calculated using sample mean, is denoted by (s). | When calculated using population mean, is denoted by (σ). |
Definition of Sample Mean
The sample mean is the mean calculated from a group of random variables, drawn from the population. It is regarded as an efficient and unbiased estimator of population mean which means that the most expected value for the sample statistic is the population statistic, irrespective of the sampling error. The sample mean is calculated as under:
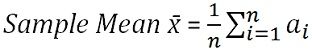where, n = Size of sample
∑ = Add up
ai = All the observations
Definition of Population Mean
In, statistics, population mean is defined as the average of the all the elements in the population. It is a mean of group characteristic, where group refers to elements of the population like items, persons, etc. and the characteristic is the item of interest. As the population is very large and not known, the population mean is unknown constant. With the help of the following formula, population mean can be calculated,
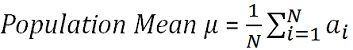where N = Size of the population
∑ = Add up
ai = All the observations
Key Differences Between Sample Mean and Population Mean
The significant differences between sample mean and population mean are explained in detail in the points given below:
- The arithmetic mean of random sample values drawn from the population is called sample mean. The arithmetic mean of the entire population is called population mean.
- The sample is represented by x̄ (pronounced as an x bar). On the other hand, population mean is labelled as μ (Greek term mu).
- While the calculation of sample mean is easy, as the list of elements provided are only few which consumes very less time. As opposed to the population mean, where the calculation is difficult, as there are many elements in population which take a lot of time.
- The accuracy of a population mean is comparatively higher than the sample mean. The accuracy of a sample mean can be enhanced by increasing the number of observations.
- Elements of the population are represented by ‘N’ in population mean. On the contrary, ‘n’ in sample mean represents the size of the sample.
- When the standard deviation is calculated using sample mean, it is denoted by letter ‘s’. Conversely, when population mean is used in the calculation of standard deviation, it is represented by sigma (σ).
Conclusion
The method of calculation of both the means are same, i.e. sum of all observations divided by the number of observations, but there is a big difference between how they are represented. While a sample mean is written as x̄ or sometimes M, population mean is labelled as μ. The sample mean is a random variable while population mean is an unknown constant.
Leave a Reply