 Probability is a mathematical concept, which has now become a full-fledged discipline and is a vital part of statistics. Random experiment in probability is a performance that generates a certain outcome, purely based on chance. The results of a random experiment are called event. In probability, there are various types of events, as in simple, compound, mutually exclusive, exhaustive, independent, dependent, equally likely, etc. When events cannot occur at the same time, they are called mutually exclusive
Probability is a mathematical concept, which has now become a full-fledged discipline and is a vital part of statistics. Random experiment in probability is a performance that generates a certain outcome, purely based on chance. The results of a random experiment are called event. In probability, there are various types of events, as in simple, compound, mutually exclusive, exhaustive, independent, dependent, equally likely, etc. When events cannot occur at the same time, they are called mutually exclusive
On the other hand, if each event is unaffected by other events, they are called independent events. Take a full read of the article presented below to have a better understanding of the difference between mutually exclusive and independent events.
Content: Mutually Exclusive Event Vs Independent Event
Comparison Chart
| Basis for Comparison | Mutually Exclusive Events | Independent Events |
|---|---|---|
| Meaning | Two events are said to be mutually exclusive, when their occurrence is not simultaneous. | Two events are said to be independent, when the occurrence of one event cannot control the occurrence of other. |
| Influence | Occurrence of one event will result in the non-occurrence of the other. | Occurrence of one event will have no influence on the occurrence of the other. |
| Mathematical formula | P(A and B) = 0 | P(A and B) = P(A) P(B) |
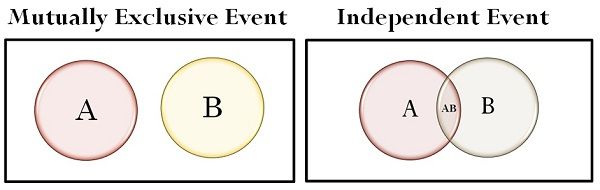
| Sets in Venn diagram | Does not overlap | Overlaps |
Definition of Mutually Exclusive Event
Mutually exclusive events are those which cannot occur concurrently, i.e. where the occurrence of one event results in non-occurrence of the other event. Such events cannot be true at the same time. Therefore, the happening of one event makes the happening of another event impossible. These are also known as disjoint events.
Let’s take an example of tossing of a coin, where the result would either be head or tail. Both head and tail cannot occur simultaneously. Take another example, suppose if a company wants to purchase machinery, for which it has two options Machine A and B. The machine which is cost effective and productivity is better, will be selected. The acceptance of machine A will automatically result in the rejection of machine B and vice versa.
Definition of Independent Event
As the name suggests, independent events are the events, in which the probability of one event does not control the probability of the occurrence of the other event. The happening or non-happening of such an event has absolutely no effect on the happening or non-happening of another event. The product of their separate probabilities is equal to the probability that both events will occur.
Let’s take an example, suppose if a coin is tossed twice, tail in the first chance and tail in the second, the events are independent. Another example for this, Suppose if a dice is rolled twice, 5 in the first chance and 2 in the second, the events are independent.
Key Difference Between Mutually Exclusive and Independent Events
The significant differences between mutually exclusive and independent events are elaborated as under:
- Mutually exclusive events are those events when their occurrence is not simultaneous. When the occurrence of one event cannot control the occurrence of other, such events are called independent event.
- In mutually exclusive events, the occurrence of one event will result in the non-occurrence of the other. Conversely, in independent events, occurrence of one event will have no influence on the occurrence of the other.
- Mutually exclusive events are represented mathematically as P(A and B) = 0 while independent events are represented as P (A and B) = P(A) P(B).
- In a Venn diagram, the sets do not overlap each other, in the case of mutually exclusive events while if we talk about independent events the sets overlap.
Conclusion
So, with the above discussion, it is quite clear that both the events are not same. Moreover, there is a point to remember, and that is if an event is mutually exclusive, then it cannot be independent and vice versa. If two events A and B are mutually exclusive, then they can be expressed as P(AUB)=P(A)+P(B) while if the same variables are independent then they can be expressed as P(A∩B) = P(A) P(B).





BALASUBRAMANIAN P says
Thanks a lot..Clear explanations.
Mahira says
Thank you very much. It’s clear
Sumit says
very well explained
Niroshan says
Great explanation
Thank you very much.
Afeima.Faafe says
Thanks