Difference Between Percentage and Percentile

The term ‘percentage‘ is widely used to express anything, from changes in the tax rates, to the rate of unemployment, to the number of people using smartphones, to resource allocation by the government, to the change in price or quantity of a product or results of an examination. It is a form of writing any digit with denominator 100.

The terms ‘percentage’ and ‘percentile’ often confuse us, especially to the students appearing in different examinations. For a given dataset, percentile represents that value in the distribution or level, at or below which, a certain percentage of score lies.

In this post, you will come to know exactly what differentiates the two.

Content: Percentage Vs Percentile

1. Comparison Chart
2. Definition
3. Key Differences
4. Examples
5. Conclusion

Comparison Chart

Basis for Comparison	Percentage	Percentile
Meaning	The percentage refers to the unit of measurement indicating, for every hundred.	Percentile implies a value, at or below which a specific proportion of the observations lies.
What does it depict?	Scores out of hundred, or per hundred	Position or standing on the basis of appearance
Represents	Rate, number or amount	Rank
Symbol	%	pth
Based on	Individual performance	Relative performance
Comparison of	Actual scores with the total scores.	Individual's rank with the total number of students who appeared the examination.
Objective	To show fractional numbers as whole numbers.	To show where the scores stand in relation to other scores.
Quartiles	No	Yes
Based on the normal frequency distribution	No	Yes

Definition of Percentage

The word ‘percentage’ is a combination of two words, ‘per’ ‘cent’, i.e. ‘per hundred’ or ‘/100’, signifying ‘out of 100’. In mathematical terminology, ‘out of’ refers to ‘divide by’. For instance, 30% denotes 30 per 100, which can be expressed as a fraction (30/100), or as a decimal (0.30).

Hence, we can use the given rule to convert a number stated in percentage terms, into fraction or decimal: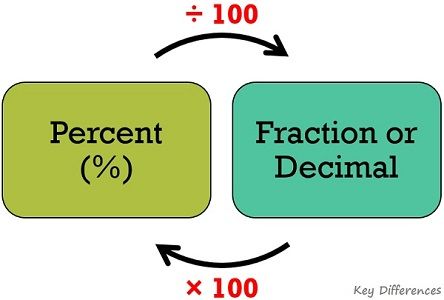

To convert a fraction into a percentage, all you need to do is divide the numerator by the denominator and multiply the result by 100.

For example:

• Suppose if 60% of people in India are using Amazon for online shopping, then it means that if there are possibly 100 people in total, 60 people would use Amazon to shop online.
• A person donates 15% of his income to the orphanage. This implies that 15 out of every 100 rupees of his income is donated.

Ratio Comparison

The percentage can also be used to compare ratios by representing them as percentages.
For example:

• In two exams, 420 out of 500 and 355 out of 400 candidates were present. Now, we can express and compare the present percentage as:
  In the first exam,
  420 out of 500 candidates appeared = (420/500)×100 = 84%
  In the second exam,
  370 out of 400 candidates appeared = (355/400)×100 = 88.75%

Definition of Percentile

In statistics, percentile refers to the point on a measurement scale, at or below which a specified percentage of the cases lies. The percentile rank of a score, implies the proportion of scores in a frequency distribution, that the marks obtained are more than or equal to. It reflects how a score compared to other scores in the given dataset.

Alternatively, it can also refer to the values which divide the dataset into 100 equal parts.

For example:

• Suppose a student obtained 85 marks in an exam and this marks is higher than or equal to marks of 79% of the students who gave the exam, then the percentile rank of the student would be 79.
• In a group of 15 people, Robin is the 3^rd oldest person. 80% of the people are younger than Robin. 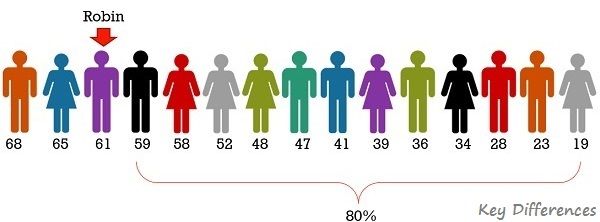This indicates that Robin is at 81^th percentile. Hence, the age of Robin, i.e. 61 years is the 80th percentile age in that dataset.
• The height of Alex is 168 cm, who is 5^th tallest person in the group of 40 people. This put him in 87.5^th percentile. This implies that the height of 87.5% of the people in the group is equal to or less than 168 cm

Hence, in an examination, the range of percentile rank shown in the result indicates the range within which the candidate’s ‘true’ percentile rank takes place.

Example 1

Suppose Arya scored 560 marks in an exam out of 700. So, the percentage would be:
Maximum Marks: 700
Marks Obtained: 560
Percentage:

Now, we will understand percentile, using the same example.

Let us suppose, the total students applied for the exam were 1,00,000 while the total students appeared in the exam were 80,000, out of which 65,000 students got marks less than 560. So the percentile will be:
This means that 81.25 scored marks lower than Arya.

Example 2

Percentage	Percentile
Total Marks = 800	Obtained Percentage = 90%
Marks obtained in different subjects = 81, 85, 93, 97, 86, 92, 91 and 95	Total students applied and appeared for the examination = 5,00,000 and 4,50,000 respectively.
Total marks obtained = 720	Total students who got less marks than you = 3,80,000
So, out of 100 = = 90%	Percentile = = 84.45
Percentage = 90%	Percentile = 84.45
This denotes that you have got 90 marks per 100 marks.	This denotes that 84.45% of the students scored less marks than the given marks.

Conclusion

The percentage is mainly used for reporting information and also to show comparison, as the base number is always 100. On the other hand, we use percentile to know the relative standing of a value, and so it is mainly employed in the ranking system.