 Ratio and proportion are two mathematical concepts which have end number of practical applications in different spheres of life. The ratio is used to compare the quantities of two different categories like the ratio of men to women in the city. Here, men and women are the two different categories.
Ratio and proportion are two mathematical concepts which have end number of practical applications in different spheres of life. The ratio is used to compare the quantities of two different categories like the ratio of men to women in the city. Here, men and women are the two different categories.
On the contrary, Proportion is used to find out the quantity of one category over the total, like the proportion of men out of total people living in the city.
Ratio defines the quantitative relation between two amounts, representing the number of time one value contains the other. Conversely, Proportion is that part that that explains the comparative relation with the entire part. This article presents you the basic differences between ratio and proportion. Have a look.
Content: Ratio Vs Proportion
Comparison Chart
| Basis for Comparison | Ratio | Proportion |
|---|---|---|
| Meaning | Ratio refers to the comparison of two values of the same unit. | When two ratios are set equal to each other, it is called as proportion. |
| What is it? | Expression | Equation |
| Denoted by | Colon (:) sign | Double Colon (::) or Equal to (=) sign |
| Represents | Quantitative relationship between two categories. | Quantitative relationship of a category and the total |
| Keyword | 'To every' | 'Out of' |
Definition of Ratio
In mathematics, the ratio is described as the comparison of the size of two quantities of the same unit, which is expressed in terms of times i.e. the number of times the first value contains the second. It is expressed in its simplest form. The two quantities under comparison are called the terms of ratio, where the first term is antecedent and the second term is consequent.
For example: 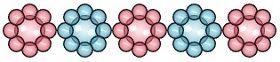 In the given figure, there are 3 red flower to 2 blue flowers, i.e. 3 : 2. So 3 and 2 are two quantities of the same unit, the fraction of these two quantities (3/2) is known as its ratio. Here, 3 & 2 are the terms of the ratio, where 3 is antecedent while 2 is consequent.
In the given figure, there are 3 red flower to 2 blue flowers, i.e. 3 : 2. So 3 and 2 are two quantities of the same unit, the fraction of these two quantities (3/2) is known as its ratio. Here, 3 & 2 are the terms of the ratio, where 3 is antecedent while 2 is consequent.
There are few points to remember in relation to ratio, which is mentioned as under:
- Both antecedent and consequent can be multiplied by the same number. The number should be non-zero.
- The order of the terms is significant.
- The existence of ratio is only between the quantities of the same kind.
- The unit of the quantities under comparison should also be same.
- Comparison of two ratios can only be done if they are in equivalent like the fraction.
Definition of Proportion
Proportion is a mathematical concept, which states the equality of two ratios or fractions. It refers to some a category over the total. When two sets of numbers, increase or decrease in the same ratio, they are said to be directly proportional to each other.
For example,  1 out of 3 flowers is red = 2 out of 6 flowers is red.
1 out of 3 flowers is red = 2 out of 6 flowers is red.
Four numbers p, q, r, s are considered to be in proportion if p : q = r : s, then p/q = r/s, i.e. ps = qr (by cross multiplication rule). Here p, q, r, s are called the terms of proportion, wherein p is the first term, q is the second term, r is the third term, and s is the fourth term. The first and fourth term are called extremes while the second and third term are called means i.e. middle term. Further, if there are three quantities in continuous proportion, then the second quantity is the mean proportion between the first and third quantity.
Important properties of proportion are discussed below:
- Invertendo – If p : q = r : s, then q : p = s : r
- Alternendo – If p : q = r : s, then p : r = q : s
- Componendo – If p : q = r : s, then p + q : q = r + s : s
- Dividendo – If p : q = r : s, then p – q : q = r – s : s
- Componendo and dividendo – If p : q = r : s, then p + q : p – q = r + s : r – s
- Addendo – If p : q = r : s, then p + r : q + s
- Subtrahendo – If p : q = r : s, then p – r : q – s
Key Differences Between Ratio and Proportion
The difference between ratio and proportion can be drawn clearly on the following grounds:
- Ratio is defined as the comparison of sizes of two quantities of the same unit. Proportion, on the other hand, refers to the equality of two ratios.
- The ratio is an expression while proportion is an equation which can be solved.
- The ratio is represented by Colon (:) sign between the quantities compared. In contrast proportion, is denoted by Double Colon (::) or Equal to (=) sign, between the ratios under comparison.
- The ratio represents the quantitative relationship between two categories. As opposed to proportion, which shows the quantitative relationship of a category with the total.
- In a given problem, you can identify whether they are in ratio or proportion, with the help of keywords they use i.e. ‘to every’ in ratio and ‘out of’ in the case of proportion.
Example
There are total 80 students in class, out of which 30 are boys and rest of the students are girls. Now find out the following:
(i) Ratio of boys to girls and girls to boys
(ii) Proportion of boys and girls in the class
Solution: (i) Ratio of boys to girls = Boys:Girls = 30:50 or 3 : 5
Ratio of girls to boys = Girls: Boys = 50 : 30 or 5 : 3
Thus, For every three boys there are five girls or for every five girls, there are three boys.
(ii) Proportion of boys = 30/80 or 3/8
Proportion of girls = 50/80 or 5/8
Thus, 3 in every 8 students is a boy and 5 in every 8 students is a girl.
Conclusion
Therefore, with the above discussion and examples, one can easily understand the differences between these two mathematical concepts. The ratio is the comparison of two numbers while proportion is nothing but an extension over ratio which states that two ratios or fraction are equivalent.




Asad Ur rahman says
Very clear and easy to understand in a moment
the stark says
That’s a very nice explanation Ma’am. keep up the good work.
Laksh Kumar soni says
It is very important to children and very informative it is also interesting
gandu says
if i present 20 questionnaire 25%, 25%,25%,25% are always, often, some and very fair. how do I present this percentages in number. is it using proportion or ratio? for example 25% 0f 20 is 5. please explain asap.
JHEALYN says
THANK YOU FOR THE INFORMATION. GOD BLESS