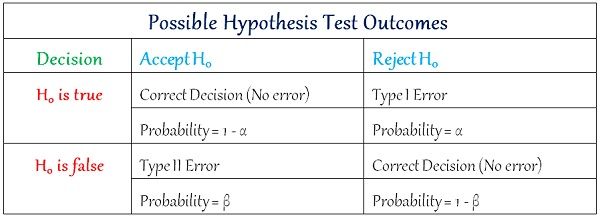
There are primarily two types of errors that occur, while hypothesis testing is performed, i.e. either the researcher rejects H0, when H0 is true, or he/she accepts H0 when in reality H0 is false. So, the former represents type I error and the latter is an indicator of type II error.
The testing of hypothesis is a common procedure; that researcher use to prove the validity, that determines whether a specific hypothesis is correct or not. The result of testing is a cornerstone for accepting or rejecting the null hypothesis (H0). The null hypothesis is a proposition; that does not expect any difference or effect. An alternative hypothesis (H1) is a premise that expects some difference or effect.
There are slight and subtle differences between type I and type II errors, that we are going to discuss in this article.
Content: Type I Error Vs Type II Error
Comparison Chart
| Basis for Comparison | Type I Error | Type II Error |
|---|---|---|
| Meaning | Type I error refers to non-acceptance of hypothesis which ought to be accepted. | Type II error is the acceptance of hypothesis which ought to be rejected. |
| Equivalent to | False positive | False negative |
| What is it? | It is incorrect rejection of true null hypothesis. | It is incorrect acceptance of false null hypothesis. |
| Represents | A false hit | A miss |
| Probability of committing error | Equals the level of significance. | Equals the power of test. |
| Indicated by | Greek letter 'α' | Greek letter 'β' |
Definition of Type I Error
In statistics, type I error is defined as an error that occurs when the sample results cause the rejection of the null hypothesis, in spite of the fact that it is true. In simple terms, the error of agreeing to the alternative hypothesis, when the results can be ascribed to chance.
Also known as the alpha error, it leads the researcher to infer that there is a variation between two observances when they are identical. The likelihood of type I error, is equal to the level of significance, that the researcher sets for his test. Here the level of significance refers to the chances of making type I error.
E.g. Suppose on the basis of data, the research team of a firm concluded that more than 50% of the total customers like the new service started by the company, which is, in fact, less than 50%.
Definition of Type II Error
When on the basis of data, the null hypothesis is accepted, when it is actually false, then this kind of error is known as Type II Error. It arises when the researcher fails to deny the false null hypothesis. It is denoted by Greek letter ‘beta (β)’ and often known as beta error.
Type II error is the failure of the researcher in agreeing to an alternative hypothesis, although it is true. It validates a proposition; that ought to be refused. The researcher concludes that the two observances are identical when in fact they are not.
The likelihood of making such error is analogous to the power of the test. Here, the power of test alludes to the probability of rejecting of the null hypothesis, which is false and needs to be rejected. As the sample size increases, the power of test also increases, that results in the reduction in risk of making type II error.
E.g. Suppose on the basis of sample results, the research team of an organisation claims that less than 50% of the total customers like the new service started by the company, which is, in fact, greater than 50%.
Key Differences Between Type I and Type II Error
The points given below are substantial so far as the differences between type I and type II error is concerned:
- Type I error is an error that takes place when the outcome is a rejection of null hypothesis which is, in fact, true. Type II error occurs when the sample results in the acceptance of null hypothesis, which is actually false.
- Type I error or otherwise known as false positives, in essence, the positive result is equivalent to the refusal of the null hypothesis. In contrast, Type II error is also known as false negatives, i.e. negative result, leads to the acceptance of the null hypothesis.
- When the null hypothesis is true but mistakenly rejected, it is type I error. As against this, when the null hypothesis is false but erroneously accepted, it is type II error.
- Type I error tends to assert something that is not really present, i.e. it is a false hit. On the contrary, type II error fails in identifying something, that is present, i.e. it is a miss.
- The probability of committing type I error is the sample as the level of significance. Conversely, the likelihood of committing type II error is same as the power of the test.
- Greek letter ‘α’ indicates type I error. Unlike, type II error which is denoted by Greek letter ‘β’.
Possible Outcomes
Conclusion
By and large, Type I error crops up when the researcher notice some difference, when in fact, there is none, whereas type II error arises when the researcher does not discover any difference when in truth there is one. The occurrence of the two kinds of errors is very common as they are a part of testing process. These two errors cannot be removed completely but can be reduced to a certain level.
Sajib banik says
useful information
Tomisi says
Thanks, the simplicity of your illusrations in essay and tables is great contribution to the demystification of statistics.
Tika Ram Khatiwada says
Very simply and clearly defined.
sanjaya says
Good article..