Difference Between Area and Perimeter

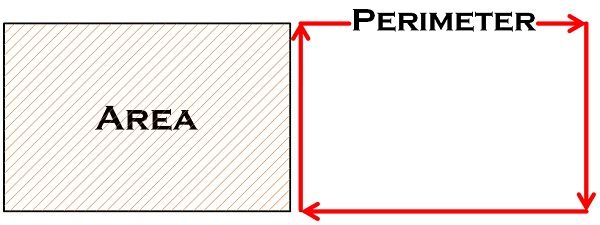
Area and perimeter are two vital fundamental concepts of mathematics, which are often understood together. These two concepts are used to measure the physical space of an object and forms a foundation for advanced mathematics. The perimeter is often understood as the length of the path that covers a closed figure while the area refers to the space covered by the closed figure.

Both the concepts have practical application and are used in our day to day life. While the area is nothing but the extent of the surface, the perimeter is the continuous line that forms a boundary of a closed geometrical shape. Take a read of the article to know the basic differences between area and perimeter.

Content: Area Vs Perimeter

1. Comparison Chart
2. Definition
3. Key Differences
4. Formulas
5. Conclusion

Comparison Chart

Basis for Comparison	Area	Perimeter
Meaning	Area is described as the measurement of the surface of the object.	Perimeter refers to the outline that surrounds a closed figure.
Represents	Space occupied by the figure.	Rim or boundary of a figure.
Measurement	Square units	Linear units
Dimensions involved	Two	One
Example	Space covered by the garden.	Length of fence required to enclose the garden.

Definition of Area

In mathematics, the area of a flat surface is defined as the amount of space covered by it. It is a physical quantity that indicates the number of square units occupied by the two-dimensional object. It is used to know how much space is taken up by a flat surface. It is measured in square units, i.e. square meters, square miles, square inches, etc.

The term area has end number of practical usage like in construction projects, farming, architecture and so on. To measure the area of a flat surface, you need to count the number of squares covered by the shape.

For instance: Suppose you need to tile the floor of the room, the number of tiles required to cover the whole room will be its area.

Definition of Perimeter

The perimeter is defined as a measure of the length of the border that surrounds a closed geometrical figure. The term ‘perimeter’ is derived from the Greek word, ‘Peri’ and ‘meter’ which means around and measure. In geometry, it implies the continuous line forming the path outside the two-dimensional shape.

In simple words, the perimeter is nothing but the length of the outline of a figure. To find out the perimeter of a particular object, you can simply add the length of the sides, to arrive at its perimeter. The perimeter of a circle is commonly known as its circumference.

For instance: a. Suppose, you wrap a string around the square, the length of the string would be its perimeter.
b. You walk around outside the garden, the distance covered would be garden’s perimeter.

Formulas

Object	Area	Perimeter	Variable
Square	a^2	4a	where, a = length of side
Rectangle	l×b	2(l+b)	where, l = length b = breadth
Circle	πr^2	2πr = πd	where, r = radius
Triangle	1/2 bh	a+b+c	where, b = base h = height a,b,c = length of the sides
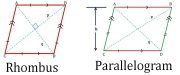
Rhombus	(pq)/2	4a	where, a = side p and q are diagonals
Parallelogram	bh	2(a+b)	where b = base h = height a = side
Trapezium	½(a+b) × h	a+b+c+d	where a = base b = base h = height c = side d = side

Conclusion

After reviewing the above points, it is quite clear that these two mathematical concepts are different, but you can use one to figure out another. While area simply means, the ‘space covered’ i.e. inside of the object, perimeter refers to the ‘distance around, i.e. the outline of the shape. Moreover, figures with the same perimeter can have different area and figures with the same area can have a different perimeter.