Difference Between Rhombus and Parallelogram

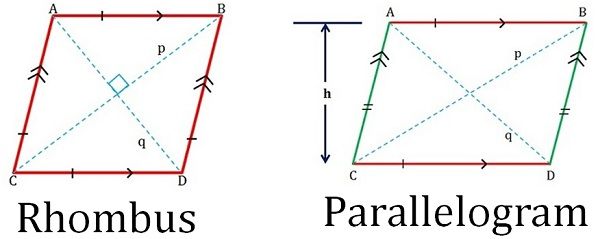
In geometry, there are many types of a quadrilateral i.e. parallelogram, rhombus, square, rectangle, trapezium, and kite, which share common characteristics, due to which people face trouble in understanding these figures. A rhombus can be referred as a slanting square, whose adjacent sides are equal. On the contrary, a parallelogram is a slanting rectangle with two sets of parallel opposite sides.

The basic difference between rhombus and parallelogram lies in their properties, i.e. all the sides of a rhombus have the same length, whereas parallelogram is a rectilinear figure whose opposite sides are parallel.

Content: Rhombus Vs Parallelogram

1. Comparison Chart
2. Definition
3. Key Differences
4. Conclusion

Comparison Chart

Basis for Comparison	Rhombus	Parallelogram
Meaning	Rhombus refers to a flat shaped, four-sided figure with all sides congruent.	A parallelogram is a four sided flat-shaped figure, whose opposite sides are parallel to each other.
Equal sides	All four sides have equal length.	Opposite sides have equal length.
Diagonals	The diagonals bisect each other at right angles forming scalene triangle.	The diagonals bisect each other forming two congruent triangle.
Area	(pq)/2, where p and q are the diagonals	bh, where b = base and h = height
Perimeter	4 a, where a = side	2 (a+b), where a = side, b = base

Definition of Rhombus

A quadrilateral whose length of its sides are congruent is called a rhombus. It is flat shaped and has four sides; wherein the facing sides are parallel to one another (see figure given below).

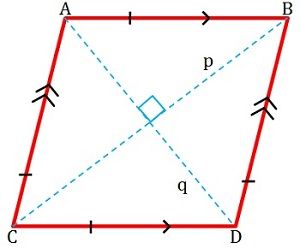The opposite angles of a rhombus are equal i.e. of the same degree. Its diagonals meet each other at 90 degrees (right angle), therefore, perpendicular to each other and forms two equilateral triangles. Its adjacent sides are supplementary, which means that the sum of their measure is equal to 180 degrees. It is also known as an equilateral parallelogram.

Definition of Parallelogram

A parallelogram as its name suggests is a is described as a flat shaped figure, having four sides whose set of opposite sides are parallel and congruent (see figure given below).

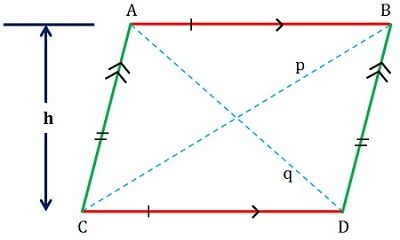The measure of its facing angles is equal and consecutive angles are supplementary, i.e. the sum of their measure equals to 180 degrees. Its diagonals bisect one another that forms two congruent triangles.

Conclusion

Both parallelogram and rhombus are quadrilateral, whose facing sides are parallel, opposite angles are equal, the sum of the interior angles is 360 degree. A rhombus itself is a special kind of parallelogram. Therefore, it can be said that every rhombus is a parallelogram, but the reverse is not possible.