 As you can see, there are many objects around us, have certain area or volume, though we do not recognise it. While the area is the region covered by the closed plane figure, the volume is the amount of space occupied by an object. The measurement of area is done in suqare metres, whereas the measurement of volume is done in cubic metres.
As you can see, there are many objects around us, have certain area or volume, though we do not recognise it. While the area is the region covered by the closed plane figure, the volume is the amount of space occupied by an object. The measurement of area is done in suqare metres, whereas the measurement of volume is done in cubic metres.
The terms area and volume are two important concepts of mensurations have a wide usage not only in mathematics but also in our day to day life. The article makes an attempt to shed light on the significant differences between area and volume. Take a look at it.
Content: Area Vs Volume
Comparison Chart
Definition of Area
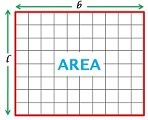
In geometry, the area of an object is nothing but its size, i.e. it is the two-dimensional space or region, which a closed figure covers. It measures the extent of space taken up by a plane object, calculated by multiplying the dimensions of the shape.
Area helps us to determine how many squares of fixed size, the shape would take to cover it. The standard unit of area, as per International System of Units (SI), is the square meters (expressed as m2). Below you can find the formula for area of various objects:
Formula:
- Area of Square = side × side
- Area of Rectangle = l × w
- Area of Parallelogram = b × h
- Area of Triangle = (b × h) / 2
- Area of Circle = πr2
where, l is the length
w is the width
h is the height
b is the base
r is the radius
Definition of Volume
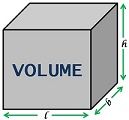
Volume refers to the amount of space inside the three-dimensional object enclosed by a closed surface, i.e. it determines the space that the shape contains. A cubic metre is the SI unit of Volume.
In simple terms, the volume of an object is nothing but its capacity. For instance, Suppose there is a hollow bottle, so the volume is the quantity of liquid it can hold. Below you can find the formula for volume of various objects:
Formula:
- Volume of Rectangular Prism = l × w × h
- Volume of Cube = a3
- Volume of Sphere = (4/3) × π × r3
- Volume of Cylinder = π × r2 × h
- Volume of Cone = π × r2 × (h/3)
where, l is the length
w is the width
h is the height
a is edge
r is the radius
h is the height
Key Differences Between Area and Volume
The point given below are significant, so far as the difference between area and volume are concerned:
- The region or space of the plane figure or object is called area. The quantity of space contained by an object is called volume.
- Plane figures have area while solid shapes have volume.
- Area describes the amount of space enclosed, whereas volume determines the capacity of solids.
- The measurement of area is done in square units, which can be centimetre, yards and so on. On the contrary, the volume is measured in cubic units.
- Shapes having two dimensions, i.e. length and width have area. As against this, shapes with three dimensions, i.e. length, width and height, have volume.
Conclusion
Therefore, with the above discussion, you might have understood clearly that the two mathematical concepts vary a lot in their usage and measurement. While the area is used to determine the space covered by the plane object, the volume is used to find out the space inside the object.




gaurav shukla says
it helped me alot in differentiating b/w area and volume you have explained nicely.
ANUPAM says
Really well explained
Poiyy says
Nicely explained. Helped in my homework.