 In mathematics, you might have heard the notions of permutation and combination end number of times, but have you ever imagined that these two are different concepts? The fundamental difference between permutation and combination is the order of objects, in permutation the order of objects is very important, i.e. the arrangement must be in the stipulated order of the number of objects, taken only some or all at a time.
In mathematics, you might have heard the notions of permutation and combination end number of times, but have you ever imagined that these two are different concepts? The fundamental difference between permutation and combination is the order of objects, in permutation the order of objects is very important, i.e. the arrangement must be in the stipulated order of the number of objects, taken only some or all at a time.
As against this, in the case of a combination, the order does not matter at all. Not only in mathematics but in practical life too, we go through with these two concepts regularly. Although, we never notice it. So, take a read of the article carefully, to know how these two concepts are different.
Content: Permutation Vs Combination
Comparison Chart
| Basis for Comparison | Permutation | Combination |
|---|---|---|
| Meaning | Permutation refers to the different ways of arranging a set of objects in a sequential order. | Combination refers to several ways of choosing items from a large set of objects, such that their order does not matters. |
| Order | Relevant | Irrelevant |
| Denotes | Arrangement | Selection |
| What is it? | Ordered elements | Unordered sets |
| Answers | How many different arrangement can be created from a given set of objects? | How many different groups can be chosen from a larger group of objects? |
| Derivation | Multiple permutation from a single combination. | Single combination from a single permutation. |
Definition of Permutation
We define permutation as different ways of arranging some or all the members of a set in a specific order. It implies all the possible arrangement or rearrangement of the given set, into distinguishable order.
For example, All possible permutation created with letters x, y, z –
- By taking all three at a time are xyz, xzy, yxz, yzx, zxy, zyx.
- By taking two at a time are xy, xz, yx, yz, zx, zy.
Total number of possible permutations of n things, taken r at a time, can be calculated as:
Definition of Combination
The combination is defined as the different ways, of selecting a group, by taking some or all the members of a set, without the following order.
For example, All possible combinations chosen with letter m, n, o –
- When three out of three letters are to be selected, then the only combination is mno
- When two out of three letters are to be selected, then the possible combinations are mn, no, om.
Total number of possible combinations of n things, taken r at a time can be calculated as:
Key Differences Between Permutation and Combination
The differences between permutation and combination are drawn clearly on the following grounds:
- The term permutation refers to several ways of arranging a set of objects in a sequential order. Combination implies several ways of choosing items from a large pool of objects, such that their order is irrelevant.
- The primary distinguishing point between these two mathematical concepts is order, placement, and position, i.e. in permutation characteristics mentioned above does matter, which does not matter in the case of the combination.
- Permutation denotes several ways to arrange things, people, digits, alphabets, colours, etc. On the other hand, combination indicates different ways of selecting menu items, food, clothes, subjects, etc.
- The permutation is nothing but an ordered combination while Combination implies unordered sets or pairing of values within specific criteria.
- Many permutations can be derived from a single combination. Conversely, only a single combination can be obtained from a single permutation.
- Permutation answers How many different arrangements can be created from a given set of objects? As opposed to the combination which explains How many different groups can be picked from a larger group of objects?
Example
Suppose, there is a situation where you have to find out the total number of possible samples of two out of three objects A, B, C. In this question, first of all, you need to understand, whether the question is related to permutation or combination and the only way to find this out is to check whether the order is important or not.
If the order is significant, then the question is related to permutation, and possible samples will be, AB, BA, BC, CB, AC, CA. Where, AB is different from BA, BC is different from CB and AC is different CA.
If the order is irrelevant, then the question is related to the combination, and the possible samples will be AB, BC and CA.
Conclusion
With the above discussion, it is clear that permutation and combination are different terms, which are used in mathematics, statistics, research and our day to day life. A point to remember, regarding these two concepts is that, for a given set of objects, permutation will always be higher than its combination.
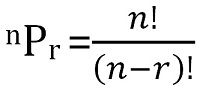
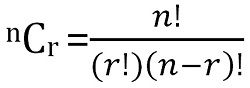




Prathmesh says
Nicely explained
Lodith Crujido Sempron says
thank you
RPA arman says
Thank You for this very nice explanation.
Hilary says
You are the best
Gabriel Emmanuel says
Thanks for this it has been helpful to me