 We use the point elasticity method when the changes in price and quantity demanded is very small. Hence, it is easy to calculate the elasticity at a point. And because changes are quite little, one can take the original price and quantity, as a base.
We use the point elasticity method when the changes in price and quantity demanded is very small. Hence, it is easy to calculate the elasticity at a point. And because changes are quite little, one can take the original price and quantity, as a base.
But, what to do when the change is substantial? One can neither take the initial price nor the final price as a base. In such a case we use the arc elasticity method, wherein we use an average of both initial and final price.
What is Elasticity?
Elasticity is the responsiveness of the quantity demanded, as a result of a change in price. In other words, it is the rate of change in the quantity demanded with respect to the rate of change in price.
When we talk about elasticity of demand we generally refer to price elasticity of demand. This is because, due to their inverse relationship, it gives a positive value. Further, when it comes to the measurement of elasticity of demand, there are three methods through which we can calculate elasticity. These are:
- Outlay method, or Total expenditure method.
- Point Method or Geometric Method
- Arc method
Also Read: Difference Between Elastic and Inelastic Demand
In this post, we will discuss the differences between point and arc elasticity
Content: Point Vs Arc Elasticity
- Comparison Chart
- What is Point Elasticity?
- What is Arc Elasticity?
- Key Differences
- Example
- Conclusion
Comparison Chart
| Basis for Comparison | Point Elasticity | Arc Elasticity |
|---|---|---|
| Meaning | Point Elasticity measures elasticity at a finite point of the demand curve. | Arc Elasticity measures elasticity at the central point of an arc between a pair of two points on the demand curve. |
| Introduced by | Marshall in 1890 | Dalton in 1920 |
| Measured when | Change is infinitesimally small | Change is finite (Discrete) |
| Uses | Derivative of supply function | Difference quotient |
| Percentage formula | Apply | Does not apply |
What is Point Elasticity?
Geometric measurement of price elasticity is possible through a method called the point elasticity method. It measures the demand at any point of the curve when the demand curve is linear.
As per this method, the price elasticity of demand of various points on the demand curve shall be different.
What is meant by the term ‘point’?
In geometry, the term ‘point’ refers to something that occupies no space and dimensions.
 Practically, point elasticity is a measure of proportionate change in quantity demanded as a result of a very small proportionate change in the price. This concept is important when the change in price and the resultant change in demand is infinitesimally small.
Practically, point elasticity is a measure of proportionate change in quantity demanded as a result of a very small proportionate change in the price. This concept is important when the change in price and the resultant change in demand is infinitesimally small.
Formula of Point Elasticity
One can use the formula given hereunder to measure elasticity:
Elasticity at different points on the Demand Curve
With the above graph we have understood that at the mid-point on the linear demand curve, elasticity equals unity. However, at the higher points on the same curve, i.e. to the left of the mid-point, elasticity will be greater than unity. Whilst, at lower points on the same curve, i.e. to the right of the midpoint, elasticity will be less than unity.
One must note that, at the corner point, i.e. end of the segment, elasticity equals zero. And, at the top, i.e. at the beginning of the segment, elasticity equals infinity.
Also Read: Difference Between Demand and Quantity Demanded
What is Arc Elasticity?
Have you ever wondered, how can we measure elasticity between two points on the same demand curve? So, we could do this through arc elasticity. For this, one has to calculate the averages of initial and final figures of price and quantity demanded.
Arc elasticity is the elasticity of a variable in relation to another between two sets of points. This is used in the absence of any general function to define the relationship between two variables. We use this concept in two domains, i.e. mathematics and economics.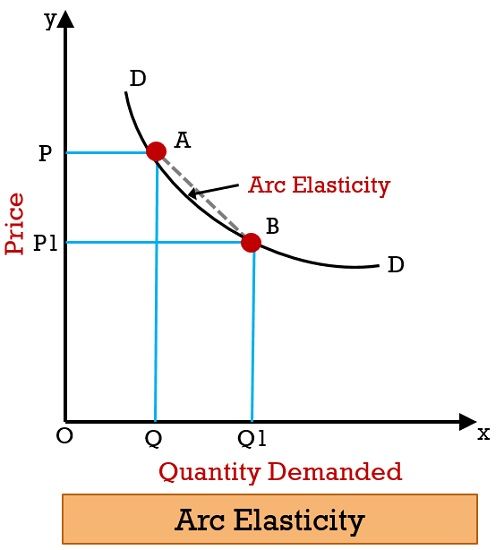
Further, we use arc elasticity to determine price elasticity over some part of the demand curve, instead of a single point. In finer terms, with the help of the arc method, we can compute elasticity over a range of prices.
Arc price elasticity of demand tends to measure the responsiveness of the quantity demanded in relation to the price of the product.
Points to Note
- We measure the elasticity over the arc of the demand curve on a graph.
- It calculates the elasticity using the central point in between two points.
- It is used when there is a substantial change in price. Also, it conveys the same elasticity outcome, even if the price decreases or increases.
When we use the Arc elasticity method?
- This method is used as a measure where the discrete figures are available for price and quantity.
- When it is possible to set apart and compute incremental changes. It depicts the movement along a portion of the demand curve.
When we have to ascertain the price elasticity between two prices or say two points on the demand curve, the question of base price pops up. That is which price we should consider as the base .As the elasticity computed by taking initial price and quantity figures as the base will be different from the one derived by taking new price and quantity figures.
Hence, to remove this confusion, we use an average of the two prices and quantities as a base.
Formula of Arc Elasticity
Where,
P1, Q1 represents the original price
P2, Q2 represents a new price
Three points should be noted:
- Arc elasticity is actually point elasticity at the central point of the arc.
- It becomes increasingly less accurate when movement is towards the arc’s end.
- The wider range, it makes the concept less useful.
Also Read: Difference Between Movement and Shift in Demand Curve
Key Differences Between Point and Arc Elasticity
In the points given below, you will find the differences between point and arc elasticity:
- Price Elasticity of Demand at a certain point on the demand curve is the point elasticity of demand. In contrast, Arc Elasticity refers to the elasticity amidst two points on the curve.
- Marshall introduced the concept of point elasticity in the year 1890. Whereas Dalton coined the concept of arc elasticity in 1920.
- The arc elasticity will always fall somewhere between pair of point elasticities, calculated at lower and higher prices. Whereas Point Elasticity is the elasticity at a finite point on the curve.
- In point elasticity, we make use of derivatives in place of finite changes in price and quantity. While in arc elasticity, we use a difference quotient.
- The percentage formula applies only in point elasticity. However, when there are finite changes in price and quantity demanded is such that it relates to a extend over the demand curve, then the percentage formula is modified is arc elasticity.
- The point elasticity method of measuring elasticity is used in case the changes in price and quantity demanded are immeasurably small. This is for the reason that such a minute change indicates a virtual point on the demand curve. As against, if there are considerable changes we use the arc elasticity method. This is because we are taking a discrete movement along an arc of the demand curve.
Example of Arc Elasticity
Suppose we need to find an elasticity of demand for a product between:
P1 = ₹1000
P2 = ₹800
Q1 = 200 units
Q2 = 300 units
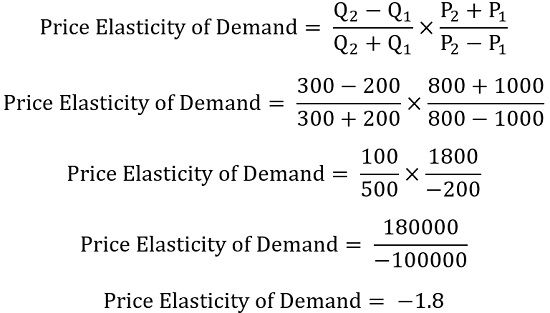
So, arc elasticity will fall somewhere point elasticity, calculated at lower and higher prices.
Conclusion
So, we have understood that the difference between point and arc elasticity lies in the size of the change in price and quantity demanded. Based on our discussion we could say that point elasticity is a marginal concept.
Therefore, it is true for small movements only from one point to another along the demand curve. Conversely, when the changes in price and quantity are discrete and large, we need to calculate elasticity over an arc of the demand curve.


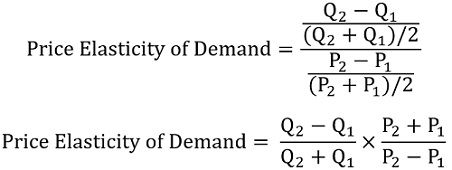





Leave a Reply