Difference Between Stratified and Cluster Sampling

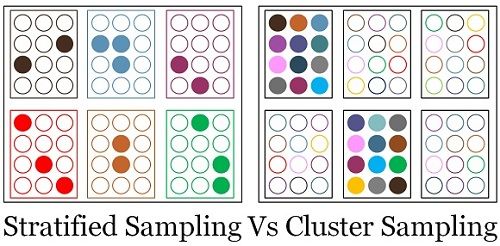
In our earlier article, we’ve discussed probability and non-probability sampling, in which we came across types of probability sampling, i.e. Stratified Sampling and Cluster Sampling. In stratified sampling technique, the sample is created out of the random selection of elements from all the strata while in the cluster sampling, all the units of the randomly selected clusters form a sample.

In stratified sampling, a two-step process is followed to divide the population into subgroups or strata. As opposed, in cluster sampling initially a partition of study objects is made into mutually exclusive and collectively exhaustive subgroups, known as a cluster. thereafter a random sample of the cluster is chosen, based on simple random sampling.

In this article excerpt, you can find all the differences between stratified and cluster sampling, so take a read.

Content: Stratified Sampling Vs Cluster Sampling

1. Comparison Chart
2. Definition
3. Key Differences
4. Video
5. Conclusion

Comparison Chart

Basis for Comparison	Stratified Sampling	Cluster Sampling
Meaning	Stratified sampling is one, in which the population is divided into homogeneous segments, and then the sample is randomly taken from the segments.	Cluster sampling refers to a sampling method wherein the members of the population are selected at random, from naturally occurring groups called 'cluster'.
Sample	Randomly selected individuals are taken from all the strata.	All the individuals are taken from randomly selected clusters.
Selection of population elements	Individually	Collectively
Homogeneity	Within group	Between groups
Heterogeneity	Between groups	Within group
Bifurcation	Imposed by the researcher	Naturally occurring groups
Objective	To increase precision and representation.	To reduce cost and improve efficiency.

Definition of Stratified Sampling

Stratified sampling is a type of probability sampling, in which first of all the population is bifurcated into various mutually exclusive, homogeneous subgroups (strata), after that, a subject is selected randomly from each group (stratum), which are then combined to form a single sample. A stratum is nothing but a homogeneous subset of the population, and when all the stratum are taken together, it is known as strata.

The common factors in which the population is separated are age, gender, income, race, religion, etc. An important point to remember is that strata should be collectively exhaustive so that no individual is left out and also non-overlapping because overlapping stratum may result in the increase in the selection chances of some population elements. The sub-types of stratified sampling are:

• Proportionate Stratified Sampling
• Disproportionate Stratified Sampling

Definition of Cluster Sampling

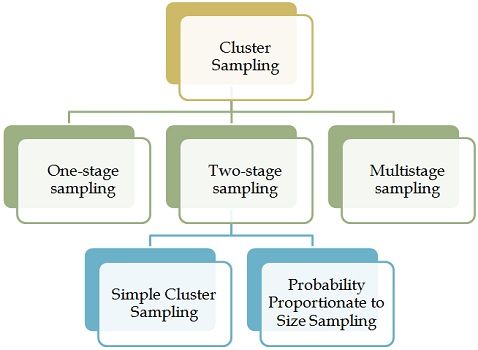
Cluster sampling is defined as a sampling technique in which the population is divided into already existing groupings (clusters), and then a sample of the cluster is selected randomly from the population. The term cluster refers to a natural, but heterogeneous, intact grouping of the members of the population.

The most common variables used in the clustering population are the geographical area, buildings, school, etc. Heterogeneity of the cluster is an important feature of an ideal cluster sample design. The types of cluster sampling are given below:

• Single-stage cluster sampling
• Two-stage cluster sampling
• Multistage cluster sampling

Video: Stratified Vs Cluster Sampling

Conclusion

To end up the discussion, we can say that a preferable situation for stratified sampling is when the identicalness within an individual stratum and the strata mean to vary from each other. On the other hand, the standard situation for cluster sampling is when the diversity within clusters and the cluster should not vary from each other.

Further, sampling errors can be reduced in stratified sampling if between-group differences among strata are increased, whereas the between-group differences among clusters should be minimised to reduce sampling errors in cluster sampling.