T-test refers to a univariate hypothesis test based on t-statistic, wherein the mean is known, and population variance is approximated from the sample. On the other hand, Z-test is also a univariate test that is based on standard normal distribution.
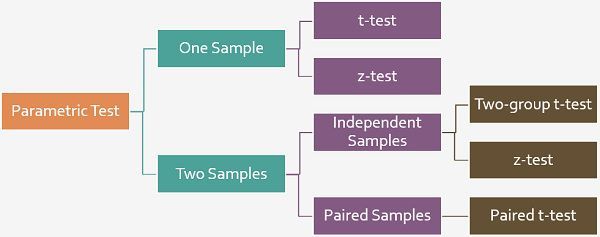
In simple terms, a hypothesis refers to a supposition which is to be accepted or rejected. There are two hypothesis testing procedures, i.e. parametric test and non-parametric test, wherein the parametric test is based on the fact that the variables are measured on an interval scale, whereas in the non-parametric test, the same is assumed to be measured on an ordinal scale. Now, in the parametric test, there can be two types of test, t-test and z-test.
This article will give you an understanding of the difference between T-test and Z-test in detail.
Content: T-test Vs Z-test
Comparison Chart
| Basis for Comparison | T-test | Z-test |
|---|---|---|
| Meaning | T-test refers to a type of parametric test that is applied to identify, how the means of two sets of data differ from one another when variance is not given. | Z-test implies a hypothesis test which ascertains if the means of two datasets are different from each other when variance is given. |
| Based on | Student-t distribution | Normal distribution |
| Population variance | Unknown | Known |
| Sample Size | Small | Large |
Definition of T-test
A t-test is a hypothesis test used by the researcher to compare population means for a variable, classified into two categories depending on the less-than interval variable. More precisely, a t-test is used to examine how the means taken from two independent samples differ.
T-test follows t-distribution, which is appropriate when the sample size is small, and the population standard deviation is not known. The shape of a t-distribution is highly affected by the degree of freedom. The degree of freedom implies the number of independent observations in a given set of observations.
Assumptions of T-test:
- All data points are independent.
- The sample size is small. Generally, a sample size exceeding 30 sample units is regarded as large, otherwise small but that should not be less than 5, to apply t-test.
- Sample values are to be taken and recorded accurately.
The test statistic is:
x ̅is the sample mean
s is sample standard deviation
n is sample size
μ is the population mean
Paired t-test: A statistical test applied when the two samples are dependent and paired observations are taken.
Definition of Z-test
Z-test refers to a univariate statistical analysis used to test the hypothesis that proportions from two independent samples differ greatly. It determines to what extent a data point is away from its mean of the data set, in standard deviation.
The researcher adopts z-test, when the population variance is known, in essence, when there is a large sample size, sample variance is deemed to be approximately equal to the population variance. In this way, it is assumed to be known, despite the fact that only sample data is available and so normal test can be applied.
Assumptions of Z-test:
- All sample observations are independent
- Sample size should be more than 30.
- Distribution of Z is normal, with a mean zero and variance 1.
The test statistic is:
x ̅is the sample mean
σ is population standard deviation
n is sample size
μ is the population mean
Key Differences Between T-test and Z-test
The difference between t-test and z-test can be drawn clearly on the following grounds:
- The t-test can be understood as a statistical test which is used to compare and analyse whether the means of the two population is different from one another or not when the standard deviation is not known. As against, Z-test is a parametric test, which is applied when the standard deviation is known, to determine, if the means of the two datasets differ from each other.
- The t-test is based on Student’s t-distribution. On the contrary, z-test relies on the assumption that the distribution of sample means is normal. Both student’s t-distribution and normal distribution appear alike, as both are symmetrical and bell-shaped. However, they differ in the sense that in a t-distribution, there is less space in the centre and more in the tails.
- One of the important conditions for adopting t-test is that population variance is unknown. Conversely, population variance should be known or assumed to be known in case of a z-test.
- Z-test is used to when the sample size is large, i.e. n > 30, and t-test is appropriate when the size of the sample is small, in the sense that n < 30.
Conclusion
By and large, t-test and z-test are almost similar tests, but the conditions for their application is different, meaning that t-test is appropriate when the size of the sample is not more than 30 units. However, if it is more than 30 units, z-test must be performed. Similarly, there are other conditions, which makes it clear that which test is to be performed in a given situation.
M.Rizwan Arshad says
nice and useful and helpful
Ana Carol says
Hey Surbhi S, I just read your article on the difference between T-test and Z-test, and I must say that it was really helpful! Your explanations were clear and concise, and I appreciated how you broke down the differences between the two tests in an easy-to-understand manner. Your comparison chart was particularly helpful in highlighting the key differences between T-test and Z-test. Thanks for sharing your knowledge on this topic with us!